Blog untuk Tugas

Nama: Wilson Nursalim
NIM: 1901516495

Rangkuman Pertemuan 9

www.binus.ac.id
www.skyconnectiva.com

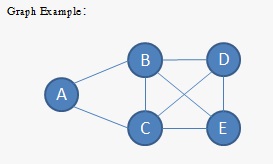
Graph

Graph adalah sebuah struktur data yang terdiri dari sekumpulan vertices dan edges.

• Vertices (nodes) adalah titik-titik pada suatu graph
• Edges adalah garis-garis yang menghubungkan suatu node dengan node lain

Degree dari suatu node adalah jumlah edges yang menghubungkan node tersebut.
Contoh:   degree dari A = 2

1. Undirected Graph
   adalah graph yang edges-nya tidak memiliki arah
2. Directed Graph
   adalah graph yang edges-nya memiliki arah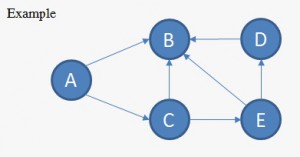
   – In Degree = Jumlah edges yang mengarah pada node tersebut
   – Out Degree = Jumlah edges yang mengarah keluar dari node tersebut

Minimum Spanning Tree adalah sebuah tree yang merepresentasikan graph dan tidak memiliki loop.

Ada beberapa cara untuk membuat minimum spanning tree dari suatu graph. Salah duanya adalah Algoritma Prim dan Algoritma Kruskal.

Algoritma Prim

1. Pilih salah satu vertex sebagai starting point Tree.
2. Hubungkan Tree dengan salah satu node yang ada di sebelahnya. Pilihlah node dengan nilai edge terkecil.
3. Lakukan terus sampai semua vertex terhubung.

Algoritma Kruskal

1. Urutkan semua edge mulai dari yang terkecil hingga terbesar.
2. Hubungkan edge yang nilainya paling kecil (bila terbentuk loop, langsung skip ke edge berikutnya).
3. Lakukan terus sampai semua vertex terhubung.

Algoritma Dijkstra

digunakan untuk mencari Shortest Path antara 2 vertex dalam suatu graph.

1. Assign to every node a tentative distance value: set it to zero for our initial node and to infinity for all other nodes.
2. Set the initial node as current. Mark all other nodes unvisited. Create a set of all the unvisited nodes called the unvisited set.
3. For the current node, consider all of its unvisited neighbors and calculate their tentative distances. Compare the newly calculated tentative distance to the current assigned value and assign the smaller one. For example, if the current node A is marked with a distance of 6, and the edge connecting it with a neighbor B has length 2, then the distance to B (through A) will be 6 + 2 = 8. If B was previously marked with a distance greater than 8 then change it to 8. Otherwise, keep the current value.
4. When we are done considering all of the neighbors of the current node, mark the current node as visited and remove it from the unvisited set. A visited node will never be checked again.
5. If the destination node has been marked visited (when planning a route between two specific nodes) or if the smallest tentative distance among the nodes in the unvisited set is infinity (when planning a complete traversal; occurs when there is no connection between the initial node and remaining unvisited nodes), then stop. The algorithm has finished.
6. Otherwise, select the unvisited node that is marked with the smallest tentative distance, set it as the new “current node”, and go back to step 3.