Blog untuk Tugas

Nama: Wilson Nursalim
NIM: 1901516495

Rangkuman Pertemuan 8

www.binus.ac.id
www.skyconnectiva.com

Heap

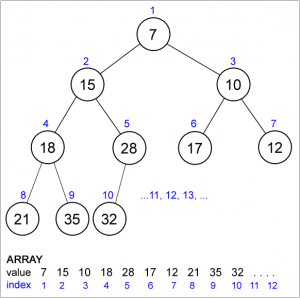
Heap adalah complete binary tree yang memenuhi syarat heap.

Min Heap

• Setiap node memiliki nilai yang lebih kecil dari nilai anaknya.
• Elemen paling kecil terletak pada Root
• Elemen paling besar terletak pada salah satu leaf

• Heaps biasanya diimplementasi dengan menggunakan array
• Setiap elemen disimpan secara berurutan mulai dari index 1 (urutannya dari atas ke bawah dan dari kiri ke kanan)
• Root disimpan pada index 1

Hubungan antar Node (anggap index node adalah x) :

• Parent(x) = x / 2
• Left-child(x) = 2 * x
• Right-child(x) = 2 * x + 1

Operasi-operasi pada Min Heap :

• find-min : untuk mencari elemen paling kecil pada heap.
• insert : untuk memasukkan elemen baru ke dalam heap.
• delete-min : untuk menghapus elemen paling kecil dari heap.

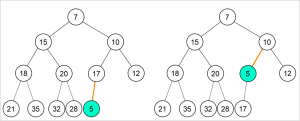
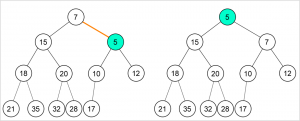
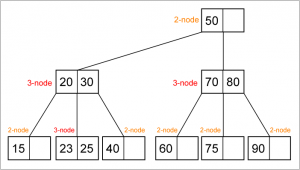
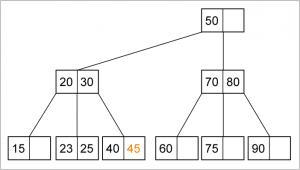
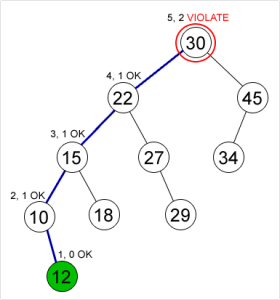
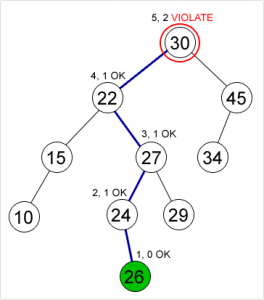
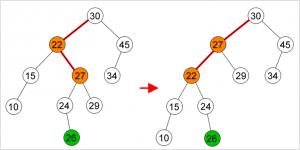
Insertion pada Min Heap :

• Masukkan elemen baru pada ujung akhir heap (setelah index dari elemen terakhir yang dimasukkan)
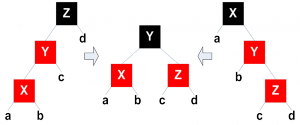
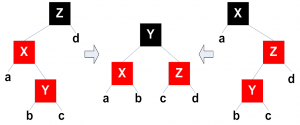
• Bandingkan nilai elemen yang dimasukkan dengan parent. Bila nilai node yang baru saja dimasukkan lebih kecil dari parent, Tukar node dengan parent. Lanjutkan proses ini ke atas sampai nilai parent lebih kecil dari nilai node atau node sudah mencapai root.

Klik gambar untuk memperbesar

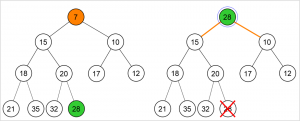
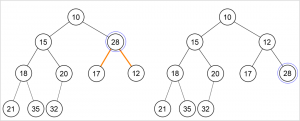
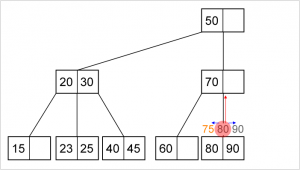
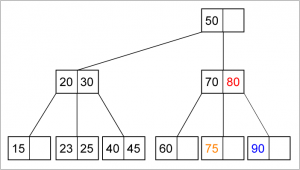
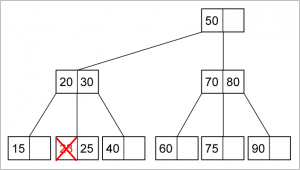
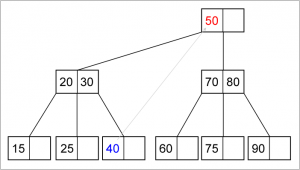
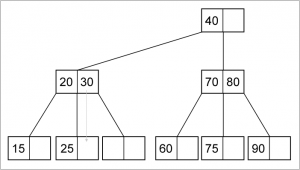
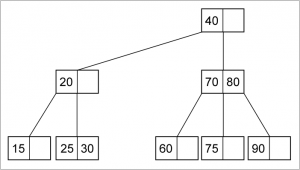
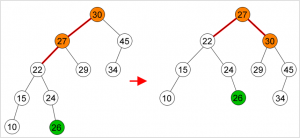
Deletion pada Min Heap :

• Gantilah root dengan elemen terakhir pada heap.
• Kurangi jumlah elemen pada heap
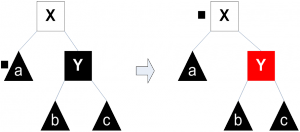
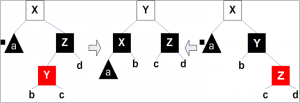
• Bandingkan nilai root dengan nilai left child dan right child. Bila ada nilai anaknya yang lebih kecil dari nilai root, Tukar root dengan anaknya (anak yang nilainya paling kecil). Lanjutkan proses ini ke bawah sampai nilai node lebih kecil dari nilai kedua anaknya atau node sudah mencapai leaf (tidak punya anak lagi).

Klik gambar untuk memperbesar

Max Heap

• Setiap node memiliki nilai yang lebih besar dari nilai anaknya.
• Elemen paling besar terletak pada Root
• Elemen paling kecil terletak pada salah satu leaf

NOTE = Max Heap memiliki sifat yang mirip dengan Min Heap, tetapi digunakan untuk mencari elemen terbesar.

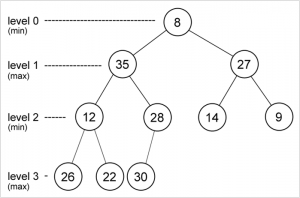
Min-Max Heap

• Kondisi heap berganti antara minimum dan maximum antar level
• Setiap elemen pada level genap lebih kecil dari anak-anaknya (min-level).
• Setiap elemen pada level ganjil lebih besar dari anak-anaknya (max-level).

• Elemen paling kecil terletak pada Root
• Elemen paling besar terletak pada salah satu anak Root (left child / right child).

Min-Max Heap memungkinkan kita dapat mencari nilai terkecil dan terbesar dari Heap pada waktu yang sama.

Insertion pada Min-Max Heap :

• Masukkan elemen baru pada ujung akhir heap (setelah index dari elemen terakhir yang dimasukkan)
• Bila node baru terletak pada min-level :
  – Jika node baru lebih besar dari parent, Tukar nilai node dengan parent, lalu Upheapmax dari parent.
  – Else: Upheapmin node baru
• Bila node baru terletak pada max-level :
  – Jika node baru lebih kecil dari parent, Tukar nilai node dengan parent, lalu Upheapmin dari parent.
  – Else: Upheapmax node baru

---

 

< Upheapmin >

• Bandingkan nilai node dengan grand-parent. Bila nilai node lebih kecil, Tukar nilai node dengan grand-parent dan Lanjutkan Upheapmin dari grand-parent.

< Upheapmax >

• Bandingkan nilai node dengan grand-parent. Bila nilai node lebih besar, Tukar nilai node dengan grand-parent dan Lanjutkan Upheapmax dari grand-parent.

 

---

Deletion pada Min-Max Heap :

-> Deletion elemen terkecil

• Gantilah root dengan elemen terakhir pada heap.
• Kurangi jumlah elemen pada heap
• Downheapmin dari Root

-> Deletion elemen terbesar

• Gantilah left child atau right child dari root (tergantung mana yang lebih besar) dengan elemen terakhir pada heap.
• Kurangi jumlah elemen pada heap
• Downheapmax dari node tersebut.

---

 

< Downheapmin >

• m adalah elemen terkecil dari antara anak-anak dan cucu-cucu dari node.
• Bila m adalah cucu dari node :
  • Jika nilai m lebih kecil dari node, maka :
    • Tukar nilai m dengan node
    • Bila sesudah ditukar nilai m lebih besar dari parent-nya, Tukar nilai m dengan parent.
    • Lanjutkan Downheapmin dari m
• Bila m adalah anak dari node :
  • Jika nilai m lebih kecil dari node, Tukar nilai m dengan node.

< Downheapmax >

• Prosesnya sama dengan Downheapmin, tetapi relational operator-nya dibalik.

 

---

 

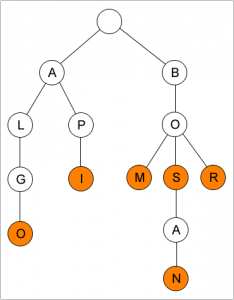
Tries 

Tries adalah struktur data Tree yang digunakan untuk menyimpan string.

Contoh:  1. Algo,   2. Api,   3. Bom,   4. Bos,   5. Bosan,   6. Bor.

Hashing

• Hashing adalah mengubah sebuah string of characters menjadi suatu key yang merepresentasikan string aslinya.
• Hashing digunakan untuk index dan mengambil item pada database karena mencari hashed key jauh lebih cepat daripada mencari original value.

h[ ]	Value
0	atan
1
2	char
3	define
4	exp
5	float
6
…
25

• Hash table adalah sebuah tabel dimana kita menyimpan original string. Index dari tabel adalah hashed key, sedangkan value yang disimpan adalah original string.
• Bila lebih dari 1 data memiliki hash-key yang sama maka terjadilah collision.

Cara menangani Collision:

• Linear Probing
  Mencari empty slot selanjutnya lalu masukkan string baru kesana.

• Chaining =
  Masukkan string ke dalam slot sebagai linked-list

 

Nama: Wilson Nursalim
NIM: 1901516495

Rangkuman Pertemuan 7

www.binus.ac.id
www.skyconnectiva.com

Red Black Tree

Red Black Tree adalah salah satu contoh self-balancing binary search tree.

Syarat Red Black Tree:

1. Setiap node mempunyai warna, hitam atau merah.
2. Warna default Root adalah hitam
3. Semua external nodes warnanya hitam
4. Node berwarna merah anaknya harus berwarna hitam
   (Tidak boleh ada node merah beranak merah)

External nodes adalah anak dari leaf. Sebenarnya external node itu cuma hayalan. Bila suatu node baru di-insert maka akan ditaruh di salah satu external node.

Insertion pada Red Black Tree

1. Masukkan node baru seperti pada BST
2. Warna node baru itu merah
3. Jika parent dari node baru itu merah, berarti terjadi violation. Kita harus memperbaiki Tree.

Contoh:  (X adalah node baru yang di-insert)

1. Bila parent dari x berwarna hitam, berarti tidak terjadi violation.
   (Tree tidak perlu diperbaiki)
2. Bila parent dan uncle dari x berwarna merah,
   Ubah warna parent dan uncle x menjadi hitam, lalu ubah warna grandparent x menjadi merah.                                                  (Click to Enlarge)
3. Bila parent dari x berwarna merah & uncle dari x berwarna hitam, (external nodes berwarna hitam)
   Maka lakukan Rotasi. Ubah pivot rotasi menjadi hitam dan anak-anaknya menjadi merah.

Single Rotation

Double Rotation

 

Deletion pada Red Black Tree

1. Lakukan deletion seperti pada BST. (Bila yang mau dihapus punya 2 anak carilah successor dari elemen paling besar di kiri atau elemen paling kecil di kanan)
2. Bila node yang mau dihapus berwarna merah, gantilah dengan anaknya yang pasti berwarna hitam.
3. Bila node yang mau dihapus berwarna hitam & anaknya merah, gantilah dengan anaknya lalu ubah warna anaknya menjadi hitam.
4. Bila node yang mau dihapus dan anaknya berwarna hitam:

• Ganti node yang mau dihapus dengan anaknya.
• Bila sibling berwarna merah, tukar warna sibling dan parent, lalu lakukan rotasi pada parent

 

 

• Bila sibling berwarna hitam dan keduanya anaknya juga hitam, maka ubah warna sibling menjadi merah

 

• Bila sibling berwarna hitam dan ada anaknya yang berwarna merah, maka lakukan rotasi

 

2-3 Tree

2-3 tree adalah struktur data dimana setiap node yang bukan leaf mempunyai:

• 2 anak dan 1 data,  atau
• 3 anak dan 2 data

Syarat 2-3 Tree:

1. Setiap node yang bukan leaf adalah 2-node (1 data dan 2 anak) atau 3-node (2 data dan 3 anak)
2. Semua data disimpan secara berurutan
3. Semua leaf ada pada level yang sama

Contoh 2-3 Tree:

Insertion pada 2-3 Tree

1. Data akan dimasukkan ke dalam salah satu leaf (diatur menurut nilainya)
2. Jika leaf tersebut merupakan 2-node, maka masukkan data kesana sehingga menjadi 3-node

   

3. Jika leaf tersebut merupakan 3-node, urutkan ketiga data, push data yang di tengah ke node parent lalu pisahkan 2 data yang tertinggal menjadi 2 buah node baru. (Perbaiki juga parent-nya secara rekursif)

Deletion pada 2-3 Tree

1. Carilah sebuah data pada leaf yang akan menggantikan data yang mau dihapus. Deletion akan selalu terjadi pada leaf.
2. Jika leaf tersebut adalah 3-node, maka hapuslah data tersebut sehingga menjadi 2-node
3. Jika leaf tersebut adalah 2-node & parent adalah 3-node, ambil satu nilai dari parent.
   – Bila sibling adalah 3-node, push satu nilai sibling ke parent sehingga parent tetap 3-node
   – Bila sibling adalah 2-node, ubah parent menjadi 2-node lalu gabungkan leaf dengan sibling
   
   
   
4. Jika leaf tersebut adalah 2-node & parent adalah 2-node,
   – Bila sibling adalah 3-node, ambil satu nilai dari parent lalu push satu nilai dari sibling ke parent
   – Bila sibling adalah 2-node, gabungkan parent dengan sibling.
5. Perbaiki parent secara rekursif bila perlu

Nama: Wilson Nursalim
NIM: 1901516495

Rangkuman Pertemuan 6

www.binus.ac.id
www.skyconnectiva.com

Bila height dari suatu Tree makin besar, maka makin lama pula waktu yang diperlukan untuk insertion, searching, dan deletion. Karena itulah kita ingin membuat Tree dengan height sekecil mungkin. Tree yang demikian adalah Balanced Binary Search Tree.

AVL Tree

(ditemukan oleh Adelson-Veleskii and E.M. Landis)

Height dari suatu node:

• Height dari sebuah empty sub tree adalah 0.
• Height dari sebuah leaf adalah 1.
• Height dari node lainnya adalah height paling besar dari anaknya ditambah dengan 1.

Balance Factor:  Selisih height anak sebelah kiri dengan anak sebelah kanan.

<NOTE> : Pada AVL Tree, Nilai  balance factor paling besar yang diperbolehkan adalah 1.

Contoh AVL Tree
(berikut dengan height & balance factor dari tiap nodenya)

---

Ketika kita memasukkan node baru ke AVL Tree, balance factor dari node lainnya bisa berubah menjadi lebih dari 1. Ketika terjadi violation seperti ini, kita perlu menyeimbangkan kembali Tree dengan melakukan rotasi.

Single Rotation

digunakan ketika:

• Node baru dimasukkan ke left sub-tree of the left child of the node that must be rebalanced (LL rotation)
• Node baru dimasukkan ke right sub tree of the right child of the node that must be rebalanced. (RR rotation)

CONTOH:

   LL rotation

Double Rotation

digunakan ketika:

• Node baru dimasukkan ke right sub tree of the left child of the node that must be rebalanced (LR rotation)
• Node baru dimasukkan ke left sub tree of the right child of the node that must be rebalanced. (RL rotation)

CONTOH:

 

LR rotation

Deletion dari suatu node pada AVL Tree juga dapat menyebabkan violation (ketika ada node yang balance factornya lebih dari 1). Tree dapat diseimbangkan kembali dengan menggunakan rotation seperti pada insertion.

---

Lecture tambahan dari dosen tamu

Click the picture to zoom in

 Tabel di atas menunjukkan perbandingan keefektifan dari tiap data structure.
Menurut dosen tamu, secara keseluruhan Tree merupakan data structure yang paling baik.